Reducing the dimensionality of data has many valuable potential uses. The low-dimensional version of the data can be used for visualisation, or for further processing in a modelling pipeline. The low-dimensional version should capture only the salient features of the data, and can indeed be seen as a form of compression. Many techniques for dimensionality reduction exists, including PCA (and its kernelized variant Kernel PCA), Locally Linear Embedding, ISOMAP, UMAP, Linear Discriminant Analysis, and t-SNE. Some of these are linear methods, while others are non-linear methods. Many of the non-linear methods falls into a class of algorithms known as manifold learning algorithms.

Architecture

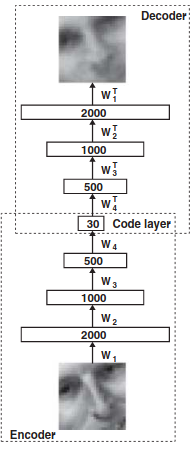
The dimensionality reduction technique discussed in this paper is based on neural networks, and is known as the autoencoder. An autoencoder is essentially a non-linear generalisation of PCA. The autoencoder architecture consists of an encoder network and decoder network, with a latent code bottleneck layer in the middle (see below figure). The goal of the encoder is to compress the input vector into a low-dimensional code that captures the salient features / information in the data. The goal of the decoder is to use that code to reconstruct an approximation of the input vector. The two networks are parameterised as multi-layer perceptrons (MLPs), and the full autoencoder (encoder + decoder) is trained end-to-end using gradient descent. Formally, the goal of an autoencoder is to minimise \(L(x, g(f(x)))\), where \(L\) is some loss function, \(f\) is the encoder network, and \(g\) is the decoder network.

rddnn1

Pre-Training

One important trick performed in the paper is pre-training of the autoencoder. This is done in order to get the weights of the network to be at a suitable initialisation such that fine-tuning is easier and more effective. The pre-training is done in a greedy, layer-wise manner (i.e. each pair of layers is pre-trained separately). This pre-training is done using a restricted Boltzmann machine (RBM).

Results

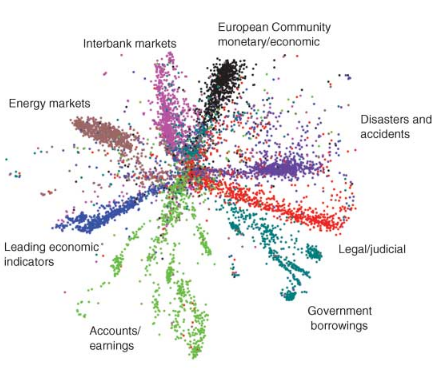
It is important to recall that an autoencoder is performing non-linear dimensionality reduction, and as such should learn a better low-dimensional data manifold than linear methods such as PCA or factor analysis. We can see a comparison between the low-dimensional representations learned by LSA and an autoencoder in the below figure (applied to documents). Clearly, the autoencoder appears to learn a better representation.

rddnn2

rddnn3