FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence
Labelled data is often either expensive or hard to obtain. As such, there has been a plethora of work to make better use of unlabelled data in machine learning, with paradigms such as unsupervised learning, semi-supervised learning, and more recently, self-supervised learning. FixMatch is an approach to semi-supervised learning (SSL) that combines two common approaches of SSL: 1. consistency regularisation and 2. pseudo-labelling.
Consistency Regularisation
Consistency regularisation is an approach that utilises unlabelled data, and its core assumption is: the model should output similar predictions when fed perturbed versions of the same input sample. Formally, what this means is that given a model \(f\) and input sample \(x\), \(f(x) = f(a(x))\) for some perturbation function \(a\). For example, for a given image, the model should return the same prediction for any perturbed version of that image (e.g. colour jittering, or affine transform).
The vanilla loss term when enforcing consistency is given by:
\[\sum_i ||p(y_i | \alpha(u_i)) - p(y_i | \alpha(u_i))||_2^2\]where \(p\) is the model, \(u_i\) is an unlabelled example, and \(\alpha\) is a stochastic perturbation function. The \(L_2\)-norm can be swapped out for other norms or metrics, but the key idea is that perturbed versions of the same input should produce similar predictions.
Pseudo-Labelling
The idea behind pseudo-labeling is to use the model itself to produce artificial labels for unlabelled data. Such pseudo-labels are usually made to be hard labels (i.e. argmax of the model’s predicted class distribution), since this encourages the model to be confident in its predictions.
The vanilla loss term when employing pseudo-labelling is given by:
\[\sum_i 1\{\max(q_i) \ge \tau\} H(\hat{q}_i, q_i)\]where \(q_i = p(y_i \vert u_i)\), \(\hat{q}_i = \text{argmax}(q_i)\) is a one-hot pseudo-label, \(H\) is cross-entropy, and \(\tau\) is a threshold parameter.
The Model
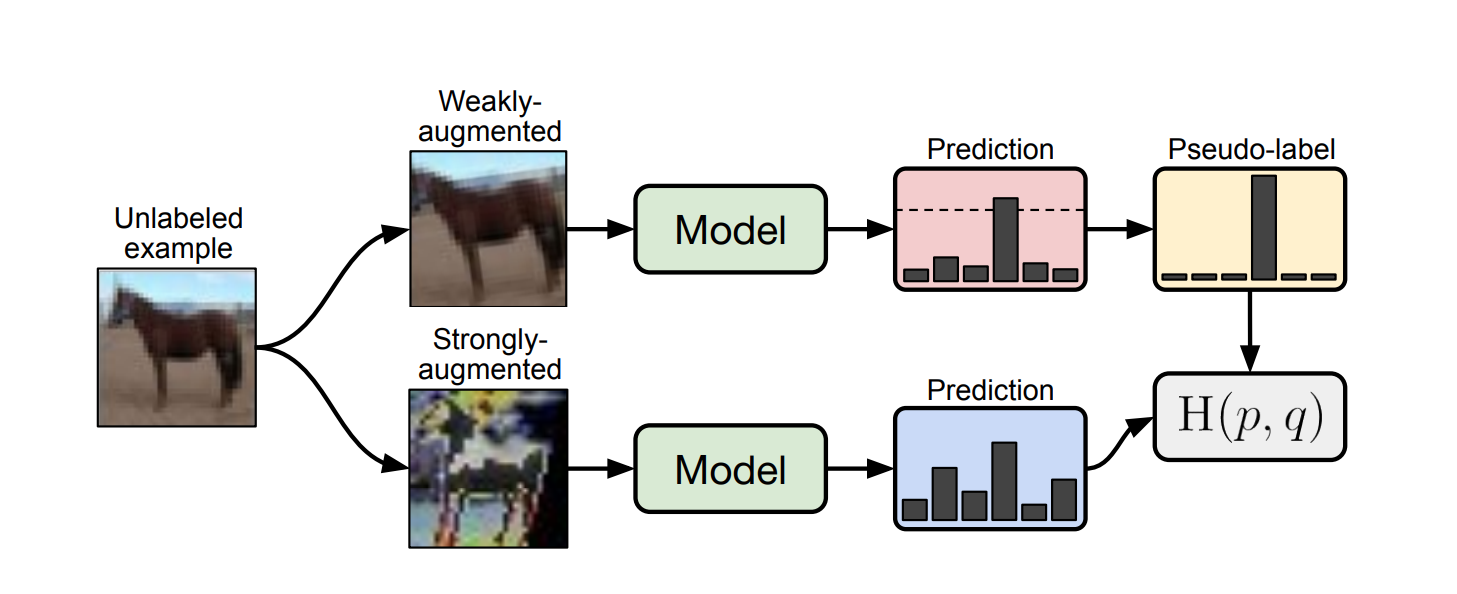
Consistency regularisation is enforced through the use of two data augmentation strategies. The first is weak augmentation, which is a simple flip-and-shift strategy whereby images are randomly flipped horizontally with probability \(0.5\), and randomly translated up to \(12.5\)% horizontally and vertically. The second is strong augmentation, which is implemented using either RandAugment or CTAugment. Both of these strong augmentation strategies employ a stronger form of distortion on to the source images, such as colour distortion and other affine transformations such as shearing.
Loss Function
The loss function for the FixMatch model consist of two terms: a supervised term \(l_s\) and an unsupervised term \(l_u\). Additionally, since FixMatch is an SSL algorithm, the loss is computed using a labelled batch of images, as well as a larger unlabelled batch of images. Note that \(\alpha\) is a weak augmentation function, and \(A\) is a strong augmentation function.
The supervised term is standard cross-entropy on weakly-augmented versions of the images in the batch:
\[l_s = \frac{1}{B} \sum_i H(p_i, p(y_i | \alpha(x_i)))\]where \(B\) is the number of the images in the batch, and \(x_i\) is the labelled example.
The unsupervised term relies on a model-generated pseudo-label. To compute this one-hot label, we first compute the model’s class distribution on weakly-augmented versions of the images: \(q_i = p(y_i \vert \alpha(u_i))\). The pseudo-label is then given by: \(\hat{q}_i = \text{argmax}(q_i)\). The actual loss term is then standard cross-entropy using this pseudo-label as the ground truth vs. predictions on strongly-augmented versions of the images:
\[\frac{1}{\mu B} \sum_i 1\{\max(q_i) \ge \tau\} H(\hat{q}_i, p(y_i \vert A(u_i)))\]where \(\mu \in \mathbb{N}\) (typically \(\mu > 1\)), and \(\tau\) denotes the threshold above which we will retain the generated pseudo-label.
The full final loss function is then given by \(l_s + \lambda_u l_u\), where \(\lambda_u \in \mathbb{R}\) is a parameter that controls the weight given to the unlabelled loss term.
Results
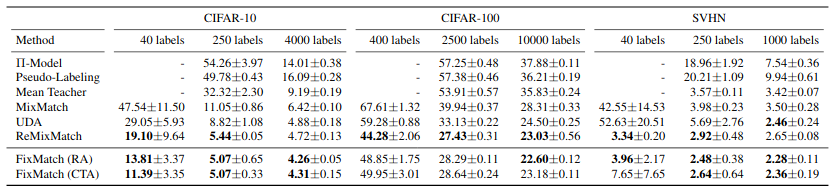
The key results from the paper can be seen in the above picture. It is also interesting to note that FixMatch manages to achieve \(78\)% accuracy on CIFAR-10 with only 1 image per class.
Important Considerations
The paper notes that careful attention has to be given to various factors of the deep learning pipeline in label-sparse settings such as SSL. In particular, SSL methods are disproportionately affected by factors such as optimiser choice, learning rate schedule, and regularisation. The recommendations from the paper include using vanilla SGD with momentum instead of Adam, weight decay regularisation (parameter norm penalties), and a specific cosine-based learning rate schedule.